محاسبه ریشه معادله با کد روش نابجایی در متلب
روش نابجایی یا معادل انگلیسی آن FalsePosition یکی از روش های محاسبات برای یافتن ریشه های یک معادله است که برای توابع پیوسته کاربرد دارد. به صورت کلی برای محاسبه ریشه های معادلات درجه دوم، سوم و چهارم روش های بسته ریاضی ارائه شده است اما برای معادلات با درجات بالاتر و پیچیده تر نیاز به آنالیزهای عددی و روش های حلقه و تکرار تا یافتن نزدیکترین جواب ممکن است. برای محاسبات این گونه معادلات معمولاً از نرم افزار متلب استفاده میشود. در این محصول کد روش نابجایی در متلب به همراه فایل راهنما استفاده از کد مربوطه و حل یک مثال برای صحت سنجی نتایج قرار داده شده است تا اگر آشنایی قبلی با این نرم افزار ندارید خیالتان از این بابت راحت باشد.
در این فایل موارد زیر پوشش داده شده است:
- کد روش نابجایی در متلب
- راهنمای گام به گام اجرای کد در نرم افزار متلب به صورت فایل PDF
- صحت سنجی کدهای نرم افزار به همراه یک مثال
الگوریتم روش نابجایی در متلب
روش نابجایی یا براکت یکی از روشهای ریشه یابی معادلات است که شباهتهایی به روش تنصیف دارد و فرض میشود که پاسخ همگرا خواهد شد.در روش نابجایی، وتری ترسیم میشود که دو نقطه a, f(a)]] و [b, f(b)] را به یکدیگر متصل میکند. سپس، نقطهای در نظر گرفته میشود که وتر، با محور x برخورد میکند و این نقطه، c نامیده میشود. مراحل این روش در زیر تشریح شده است: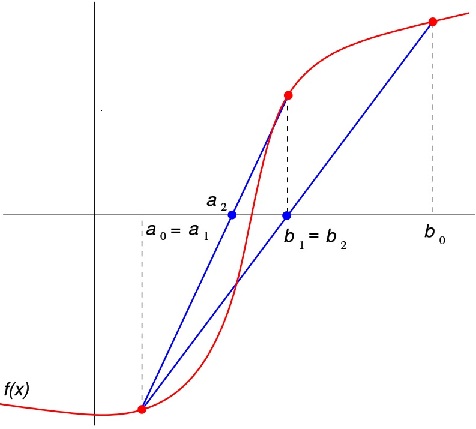
- اعداد a و b را به عنوان ابتدا و پایان بازه ای که حدس زده میشود یکی از ریشه های معادله در آن قرار داد انتخاب میشود.
- معادله خطی که دو نقطه را به یکدیگر متصل میکند، نوشته میشود.
- y – f(a) = ( (f(b)-f(a))/(b-a) )*(x-a)
- اکنون، باید نقطهای پیدا شود که با x برخورد داشته باشد، بنابراین y = 0 قرار داده میشود.
- x = (a*f(b) – b*f(a)) / (f(b)-f(a))
- این نقطه را به عنوان C انتخاب میکنیم.
- اگر f(c) == 0، پس c ریشه تابع است.
- در غیر اینصورت سه شرط بررسی میگردد:
- اگر f(a)*f(c) < 0، پس ریشه بین a و c قرار دارد. بنابراین، تکرار برای a و c انجام میشود.
- در غیر این صورت، اگر f(b)*f(c) < 0، پس ریشه بین b و c قرار دارد. بنابراین، تکرار برای b و c انجام میشود.
- تابع همگرا نیست و از این روش نمیتوان استفاده کرد.
دیگر کدهای متلب آنالیز عددی برای یافتن ریشه معادلات
در وبسایت ساخت اجرا کدهای متلب دیگری برای حل معادلات پیچیده و یافتن ریشههای آن منتشر شده است که پیشنهاد میشود بررسی کنید:
در صورتی که سوالی در ارتباط با این محصول دارید، میتوانید سوال خود را در قسمت دیدگاه این محصول مطرح بفرمائید و یا از طریق فرم تماس با ما، تیکت پشتیبانی در حساب کاربری و همچنین پشتیبانی آنلاین سایت با گروه مهندسی ساخت و اجرا در ارتباط باشید.
| تعداد فایل | تک محصول |
|---|---|
| نرم افزار | MATLAB |
| فرمت فایل | m |
در حافظه کپی شد
لینک کوتاه







Warning: file_exists(): open_basedir restriction in effect. File(/comments.php) is not within the allowed path(s): (/home/h242009/:/tmp:/var/tmp:/opt/alt/php81/usr/share/pear/:/dev/urandom:/usr/local/lib/php/:/usr/local/php81/lib/php/) in /home/h242009/domains/sakhtoejra.com/public_html/wp-includes/comment-template.php on line 1628